The paradox that links epidemiology and sociology
Why outbreaks persist and why your friends are, on average, more popular than you
In the 1970s, mathematicians noticed something strange about the spread of gonorrhea in the United States. Specifically, it shouldn’t have been possible. For the epidemic to persist, each case must have been infecting at least one other person on average. This implied each case should, on average, have at least two recent sexual partners: one who gave the infection to them, and another who they passed it onto.
But that wasn’t the reality: investigations had found that cases reported only 1.5 recent partners on average. Even if the probability of transmission during sex was very high, there didn’t seem to be enough sexual encounters happening for the disease to keep spreading. So, what was causing this apparent paradox?
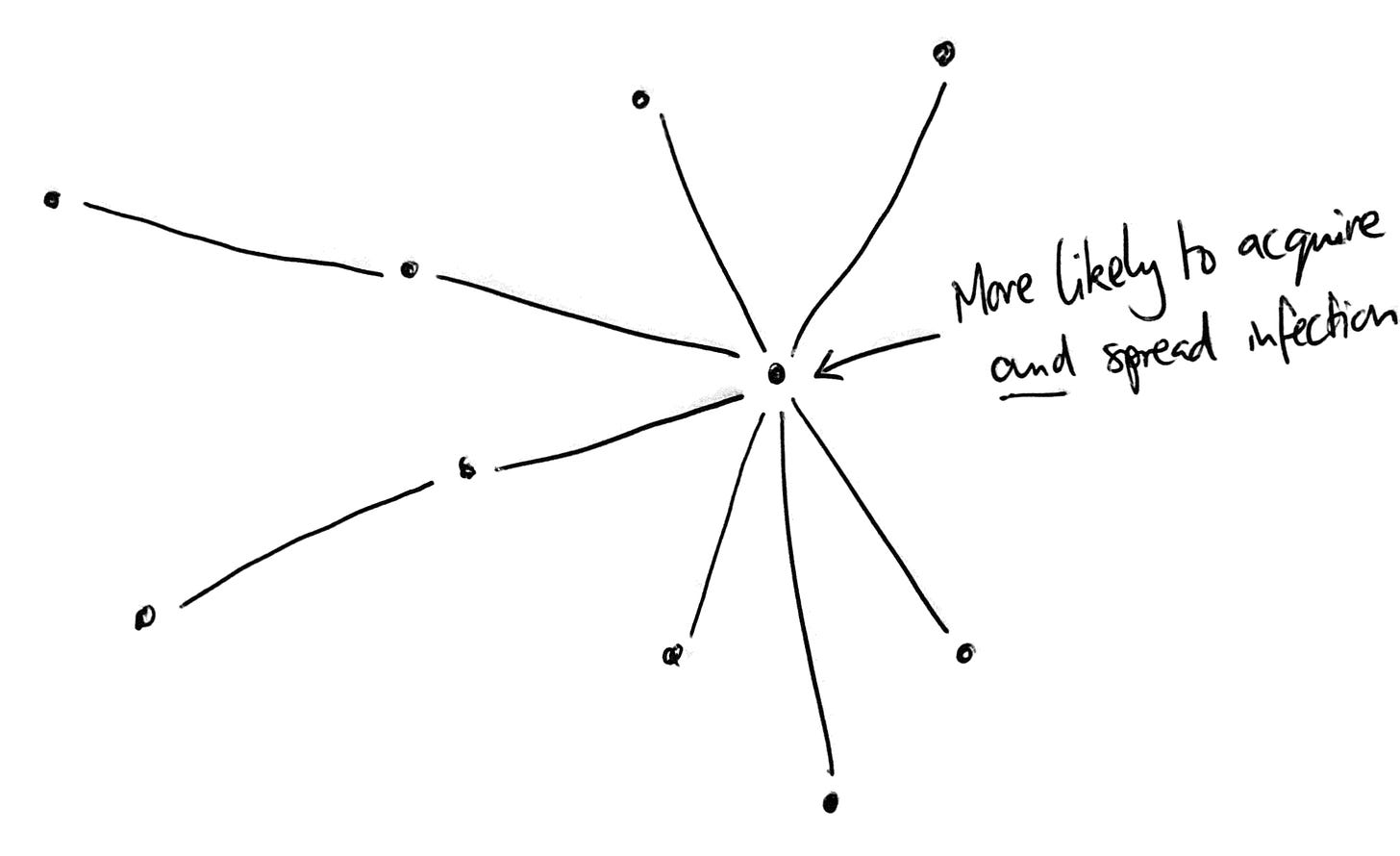
The problem turned out to be the word ‘average’. If we focus on the average number of partners, we are ignoring variability in behaviour within the population. However, this variability matters: when someone has a lot of partners, we’d expect them to be both more likely to acquire the infection and more likely to pass it on. We therefore need to account for that fact that highly connected individuals can contribute to transmission in these two different ways.
Variability explained why there was an ongoing gonorrhea epidemic, despite people having few sexual partners on average. Those with lots of contacts were contributing disproportionately to the spread, meaning that the average number of secondary cases per infectious individual (i.e. the reproduction number) was, in reality, above the crucial value of 1.
Epidemiologists Roy Anderson and Robert May would later show that the more variation there was in sexual behaviour, the higher we’d expect the reproduction number to be. If we account for the above network quirk, they calculated that the effective number of new infectious contacts (denoted by c) would depend on both the mean number of sexual partners in the population and the variance in the number of partners:
In other words, a larger variance pushes up the effective number of opportunities for transmission, and with it the effective reproduction number.
Remarkably, this network quirk would crop up in other fields as well. In 1991, sociologist Scott Feld spotted a paradox when it came to friendships: most people were less popular than their friends. If you tally up your friends, then work out how many friends each of them have on average, you will probably have fewer than they do. The same is true of other types of contacts. Chances are that your previous sexual partners have, on average, had more partners than you. If you work in academia, your co-authors probably have more papers and citations than you do. In online communities, the majority of people have fewer followers than their contacts do on average.
Why does this ‘friendship paradox’ arise? Think about your wider friendship network. It’s likely that there will be quite a bit of variability in popularity, with some people having lots of friends and some having relatively few. If you work out the average popularity of your friends, someone with lots of friends will drive up this average value. And because this person has lots of friends, they will drive up this average for a lot of people. It’s that double contribution idea again: as well as naming lots of people as friends, these popular individuals will be named by lots of people. This creates the apparent paradox, with most people in the network being less popular than their friends. As a result, Feld’s paper ended up including the exact same formula as Anderson and May (although the link was apparently not spotted at the time).
These network quirks can explain paradoxes in other areas of life too. In 1998, computer scientist Steve White noted an apparent contradiction: simple theories about the rate of computer malware growth and removal (i.e. ‘birth’ and ‘death’ rates) didn’t match the reality of viruses that could persist at low-levels for a long time:
We have a reasonable, qualitative understanding of the epidemiology of computer viruses, characterizing their spread in terms of birth rate, death rate, and the patterns of program transfer between computers. But a mystery remains. Evidence suggests that viruses are still relatively uncommon - that their prevalence has always been very low. But, according to our current theories, this can only happen if the birth rate of viruses is ever so slightly higher than their death rate, a coincidence too remarkable to believe.
In 2001, Romualdo Pastor-Satorras and Alessandro Vespignani showed that the discrepancy could be explained by network dynamics. Given the huge variability in links across computer networks, even malware that doesn’t spread easily from one device to another can survive for a suprisingly long time. In most networks, a computer is never more than a few steps from a highly connected hub, which – all things being equal – is both more likely to acquire the malware and pass it on.
Fortunately, the above network paradox can also be helpful for disease control. Take the example of human-to-human transmission. Highly connected individuals in a network might be more at risk, but it’s generally time-consuming to find them. We’d have to ask everyone to list all their contacts, then go through and work out who has more than others. However, there is a shortcut we can use. Because most people are less popular than their friends, we could instead just pick some people at random, then ask each of them to name a random friend. Thanks to the friendship paradox, this ‘random friends of random people’ method will point us to a group who are more connected than most.
What’s more, this method can be helpful when trying to spark outbreaks, such getting people to adopt health information or healthier behaviours. One 2015 study found that introducing health resources via ‘random friends of random people’ led to more uptake than just introducing it at random.
The more I’ve dug into the history of these ideas, the more I’ve been fascinated by this transition from independent inspiration to combined insight. It’s a story of how two different fields identified the same network quirk, found very different – and subsequently highly influential – applications, then found convergence in how these ideas could work in tandem. Which makes me wonder: how many useful quirks are still out there, yet to be fully realised?





Dirk Brockmann at TU Dresden does very interesting work on the way complex systems of social interaction (social networks) affect the spread of infectious disease. He was one of the most lucid commentators on the deficiencies of the early Covid modeling.