Intuition and imagination

How to explain a famous formula without just reciting facts

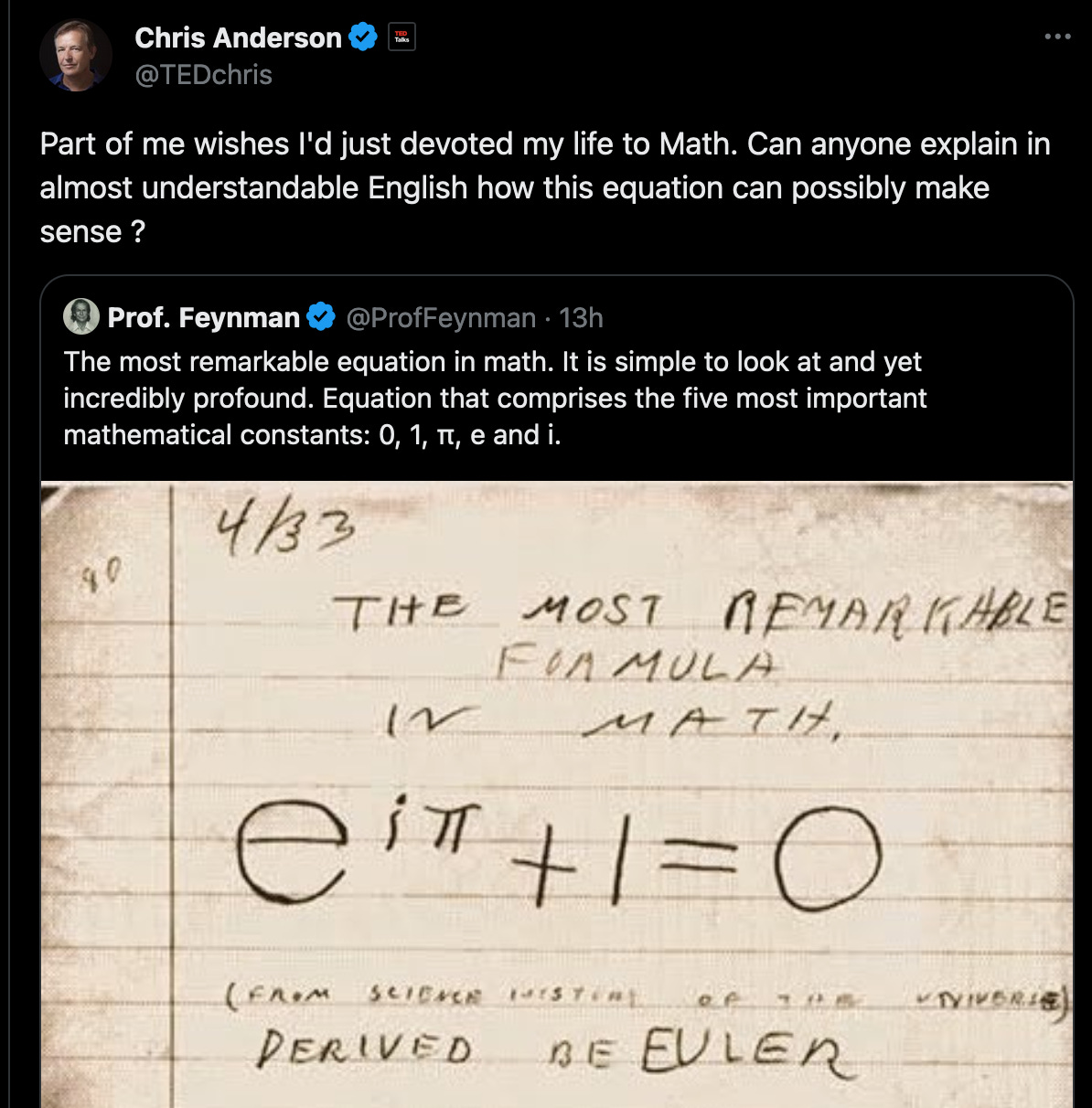
Earlier this week, I saw a nice challenge posed on Twitter. How can we explain Euler’s equation without pulling a mathematical rabbit out of a hat?

Euler’s equation, you might recall, links five key mathematical values: 0, 1, e (of logarithms), pi (of circles), and i (the imaginary number – more on this later).

For those who’ve seen the derivation from the more general Euler’s formula, it’s tempting to see the challenge and just say ‘well we write everything out and get the equation’. Or, perhaps, we might introduce some detailed background on complex numbers and complex plane, but still resort to some ‘well this is just a fact’ statements along the way.

After all, 19th century mathematician Benjamin Peirce once described the equation by saying:

it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.

Except this isn’t very satisfying for a mathematician, let alone a non-mathematician. Can we do any better?

How did they get there in the first place?

Often when I’m trying to get intuition about a mathematical or statistical concept, I turn to history. How did people back in the day manage to land on the idea?

Much of theory emerged from geometric calculations by mathematicians like Johann Bernoulli and Roger Cotes, who were focusing on arcs and circles. For example, in the early 1700s, Johann Bernoulli was trying to calculate the area of a sector of a circle centred at co-ordinates (0,0), from the horizontal line to a point (x,y). He ended up with a formula that included the square root of -1 (i.e. i) and a logarithm (i.e. the inverse of an exponential).

In other words, it was a very messy problem without a simple, intuitive answer. Eventually it simplified into something that would produce Euler’s neat equation when the point (x,y) is a half circle away from the original line. Which, admittedly, isn’t a great origin story. Is it possible to get a more satisfying explanation?

On Twitter, I suggested one possibility would be to start by noting the equation involves an exponential growth function. Then note that the ‘imaginary number’ i is weird so pulls us off the traditional number line onto a circle of radius 1 (for reasons). So if we start at x=1 and grow it by ‘pi’, we instead travel around the circle¹. Travelling a distance of ‘pi’ lands us at -1 (because the circle circumference is 2pi). So if we add 1 to -1 we get back to 0.

Which, again, is not totally satisfying as an explanation. What was I missing?

Going in circles

I realised I hadn’t gone far enough back in history. Imaginary numbers aren’t the first non-intuitive wrinkle to frustrate mathematicians. For centuries, negative numbers were avoided in European mathematics. The field was largely derived from Greek geometry, so the concept of something like ‘negative’ triangle seemed ridiculous. For example, try explaining the following equation in terms of shapes:

\(-1 \times -1 = 1\)

Tricky, isn’t it?

Societies that derived mathematics from finance did better, because debt is an easier concept to motivate negative numbers. Multiplying a debt by a debt (i.e. ‘you owe me twice what I owe you’) just switches us from the negative side of the number line to the positive.

But what about i? It’s the square root of -1, so that means:

\(i \times i = -1\)

Crucially, there is nowhere we can place i on the standard number line. We can’t stick it near 1, because 1 doesn’t behave like this, and nor does -1 (see above). So it has to exist somewhere off the number line.

But where does it exist in this imaginary, not-a-real-number world?

First, let’s think about what happens if we multiply 1 by i. This must equal i, which means we’ve started on the number line (at 1) and have now been pulled off it. But if we multiply by i again, we land back on the number line at -1. So multiplying by i somehow pulls us off the number line then back onto it.

What type of mathematical movement could do this, taking us off the line and back again in a predictable way, keeping the same distance away from zero? If we want to move and keep the same distance from a point, then the answer is we need to travel around a circle. And this is how mathematicians dealt with i, having it rotate us away from the number line on the first multiplication, then back again on the second.

So now we know how to rotate one quarter turn off the line and back again. But what if we only want to rotate a fraction of this amount? What if we want an eighth turn, for example?

Pacing ourselves

This is where e comes in. This is short for Euler’s number, and arose during the development of calculus, i.e. the study of rates of change. If we’re looking at how things change, it can be useful to have formulas that change in predictable ways, or take predictable values at certain points. For some given number x, the rate of change of e to the power of ax is equal to that same number multiplied by a:

\(\text{rate of change of } e^{ax} = ae^{ax}\)

The specific equation isn’t the main point here. What matters is that on the familiar number line, e changes at a rate proportional to itself.

But what about when i pulls us of the number line onto a circle? We get the following:

\(\text{rate of change of } e^{ix} = ie^{ix}\)

In other words, it creates a predictable relationship between i (which pulls us onto a circle) and a number x we put in (which we’ll use to control how far around the circle we go). Effectively, the combination e and i allows us to maintain an even pace as we travel around the circle by changing the value of x, rather than accelerating or decelerating in weird ways.

So if we decide we want to travel a half turn around the circle (i.e. x=pi), this gives us the following:

\(e^{i \pi} = -1 \quad \text{ which the is same as } \quad e^{i \pi} +1 = 0\)

And that’s where Euler’s equation comes from.

Hopefully that was a slightly more satisfying explanation that my original one, and much better than Peirce’s ‘we don’t know what it means’. It’s also a useful reminder than even if we know something, there can still be a lot to learn by trying to explain it intuitively to others – and ourselves.

(By the way: if you’re interested in digging into ideas like these in a slightly less equation-y way, I’ve got a new popular science book coming out next year on the topics of proof, intuition, evidence and explanation.)

1. Sorry for the clunky notation, Substack doesn’t seem to be able to format equations in paragraphs.