To understand mathematical concepts, look to history
Someone, somewhere came up with it for a reason
Want to get deeper intuition for a mathematical or statistical concept?
I find that one of the best ways is to dig into its history. Why did someone think to do it that way? Why didn’t they like what came before? How did others react to their new approach?
Take confidence intervals. These are widely misinterpreted by students and researchers. Often, they even inspire strange, circular definitions, like ‘the 95% confidence interval is the range we can be 95% confident contains the true value.’
Things can make more sense if we look at where these intervals came from. In the 1930s, economies were struggling, and governments wanted statistical insights into the lives of their populations. One such person struggling was statistician Jerzy Neyman, who was based in Poland. In 1932, he wrote a letter to a colleague: ‘I simply cannot work, the crisis and the struggle for existence takes all my time and energy.’
Economic hardship – and the need to understand its impact – would spark interest in the emerging field of ‘representative methods’. If researchers sampled a subset of the population, how confident could they be that conclusions based on this sample would be representative of the wider population?
Neyman would outline this motivation in a landmark 1934 paper:
‘This popularity of the representative method is also partly due to the general crisis, to the scarcity of money and to the necessity of carrying out statistical investigations connected with social life in a somewhat hasty way. The results are wanted in some few months, sometimes in a few weeks after the beginning of the work, and there is neither time nor money for an exhaustive research’
This period of methodological development, spearheaded by Neyman’s work, was arguably the start of modern survey research. Neyman’s big contribution in that 1934 paper was to show that probability-based sampling could, on average, produce unbiased estimates and it was possible to quantify how often such estimates would fall near the truth. This is where the confidence interval came in. If we were to hypothetically collect samples again and again, and calculate the 95% confidence interval each time, then 95% of these intervals should contain the true value:
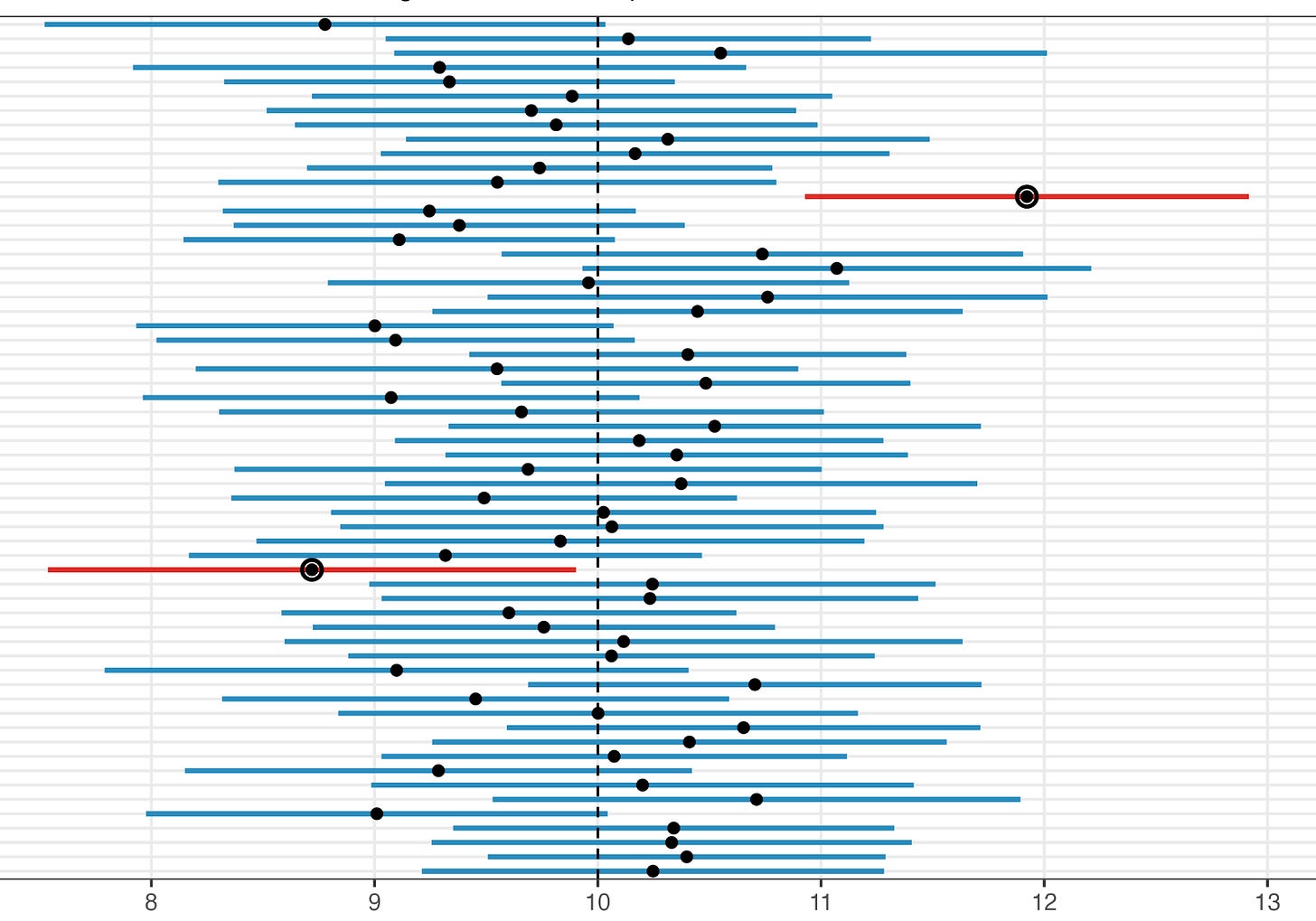
If you had to read the above definition a couple of times, you wouldn’t be the only one. Statistician Ronald Fisher would later highlight the conceptual leap required to calculate an interval based on hypothetical ‘repeat sampling’ of data, when in reality we have only collected a single sample:
‘there is always... a multiplicity of populations to each of which we can legitimately regard our sample as belonging; so the phrase ‘repeated sampling’ from the same population does not enable us to determine which population is to be used to define the probability level, for no one of them has objective reality, all being products of the statistician’s imagination.’
When Neyman announced his work on confidence intervals in 1934, his colleagues got a chance to respond in a discussion meeting at the Royal Statistical Society. The issue of knowing which hypothetical sample people had actually collected came up even then. In an accompanying critique, Arthur Bowley remarked that ‘I am not at all sure that the “confidence” is not a “confidence trick”.’
He argued that both a coincidence and a genuine phenomenon could produce the same confidence interval. Yet Neyman’s method couldn’t tell us which reality we were dealing with. ‘I think we are in the position of knowing that either an improbable event has occurred or the proportion in the population is within the limits,’ Bowley noted.
Confidence intervals aren’t just a textbook method to be rote-learned. They are part of a wider historical story, which spans everything from economic strife to philosophical arguments about what is ‘true’, what can be imagined, and what can be measured. And I think we can learn a lot by viewing the method in this broader context. As statistician Douglas Curran-Everett once put it, ‘the meaning of a confidence interval is nearly impossible to understand unless you observe the development of its underlying concept’.
If you’re interested in reading more about the history of confidence intervals and other statistical and scientific ideas, you may like my latest book Proof: The Uncertain Science of Certainty.
And if you’re interested in the conceptual journey behind ‘the most beautiful equation in maths’:
Intuition and imagination
Earlier this week, I saw a nice challenge posed on Twitter. How can we explain Euler’s equation without pulling a mathematical rabbit out of a hat?



The Austrian-American sociologist Paul Lazersfeld commonly is credited with a seminal role in creating survey research and quantitative analysis of social data. The Marienthal studies conducted in 1931-2 are often cited as the first social research of this type. Lazersfeld went on to head the Bureau of Radio Research at Columbia University. It played a critical part in bringing statistical methodology to social research, including inferential analysis of sampled social and economic data. The Bureau changed its name to the Bureau of Applied Social Research after WWII and continued until 1977.
In the private sector, George Gallup had conducted his first "poll" to predict an electoral outcome by 1932.
Work on the effects of poverty and research on communication and political influence were dominant themes of the early quantitative empirical research. This is unsurprising given the origins in Austria during the 1930s.
Adam, thank you for bringing up the importance of history on science; I think we are not (at least I am during my school years) exposed enough to this issue.
On that note, thank you for sharing "Uncertainty" with the BMJ audience; that is really. I think most of the issues you mentioned in that interview here is quite relevant to your audience in here. In case any of us want to read it; here is the link: https://www.bmj.com/content/390/bmj.r1059 (I wanted to attached the pdf I am not sure if I am allowed to do that).