Why we’re bad at understanding the strength of arguments we agree with

And how this can happen even with ‘rational’ calculations

Don’t worry, this isn’t just another post about the US election.

It’s mostly a post about coin flips, and what they can tell us about beliefs.

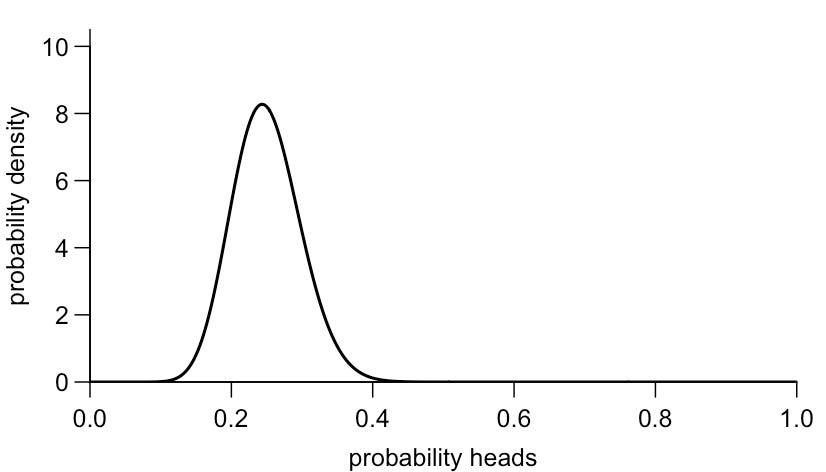
Imagine you’re holding a coin and you’re confident it’s biased. You reckon heads only comes up a quarter of the time on average, although you’re not totally sure – the probability may be a bit higher or lower. Your prior belief about the probability a flip will return heads therefore looks like the following distribution:

Now suppose you flip the coin 4 times, and 3 of these come up heads. How much should you update your belief about the coin? A bit? A lot?

Fortunately, there’s a handy formula we can use to do this calculation. (If you don’t fancy reading the maths, feel free to skip to the ‘Updating our beliefs’ section that follows.)

We can use Bayes’ theorem to relate: a) the probability that a parameter has a given value with b) the probability of observing the data given this parameter and c) our prior belief about the parameter:

\(P(\text{parameter | observed data}) = \frac{P(\text{observed data | parameter}) P(\text{parameter})}{P(\text{observed data})}\)

So in our case we have the following relationship:

\(P(\text{heads bias | data}) = \frac{P(\text{data | heads bias}) P(\text{heads bias})}{P(\text{data})}\)

The term P(heads bias | data) is known as the posterior distribution, i.e. our belief about the probability of landing on heads, once we’ve updated it with the new observations. The term P(heads bias) is our prior distribution about the coin. And P(data) tallies up all the possible ways we could generate the data, to ensure that the overall probability distribution for heads adds up to 1.

This approach can still require a fair bit of calculation, but in some situation there is a neat shortcut. In particular, if our prior is defined in terms of a beta distribution, we have what’s known as a conjugate prior. This means we can immediately get the updated posterior by adding the new events to the relevant side of the distribution.

So if our initial belief is given by the following probability distribution (i.e. 60:20 in favour of tails):

dbeta(x, 20, 60)

Then observing 3 additional heads and 1 extra tail will give us the following updated posterior:

dbeta(x, 20+3, 60+1)

Handy, right? So let’s see what effect this has.

Updating our beliefs

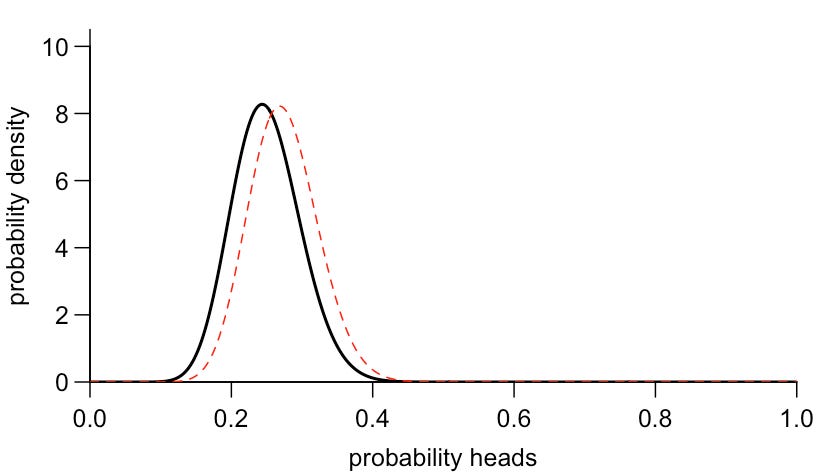
If we flip the coin 4 times, and 3 of these come up heads, Bayes’ theorem tells us that we should update our prior belief above as follows:

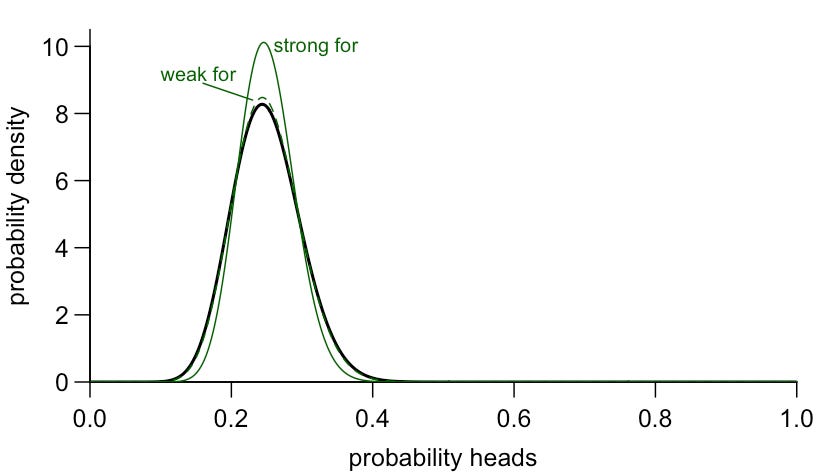
So the new information shifts the distribution a bit, but not that much. Which is perhaps not that surprising given it’s a small sample size of only 4 observations.

Next, imagine that you had flipped the coin 40 times, and 30 came up heads. This is a larger sample size, so gives us more information about the coin, and stronger evidence about the true probability of getting heads. As a result, Bayes’ theorem tells us to shift our belief further to towards heads (although not all the way to 0.75, because remember we had a strong prior belief to start with):

Assessing agreement

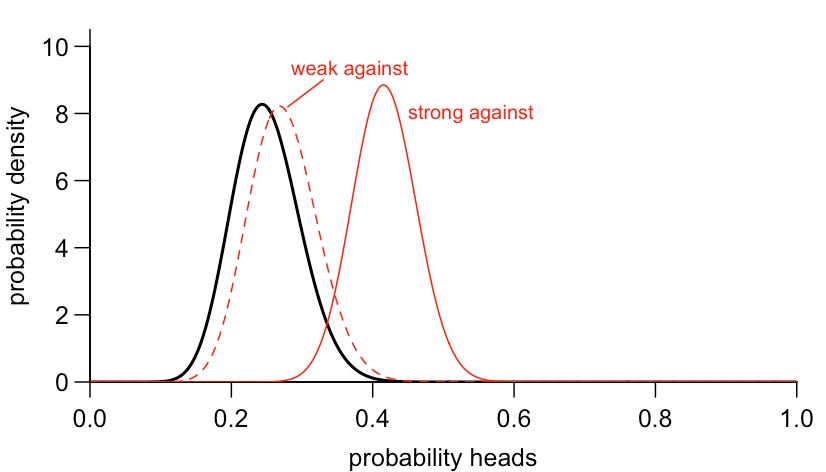
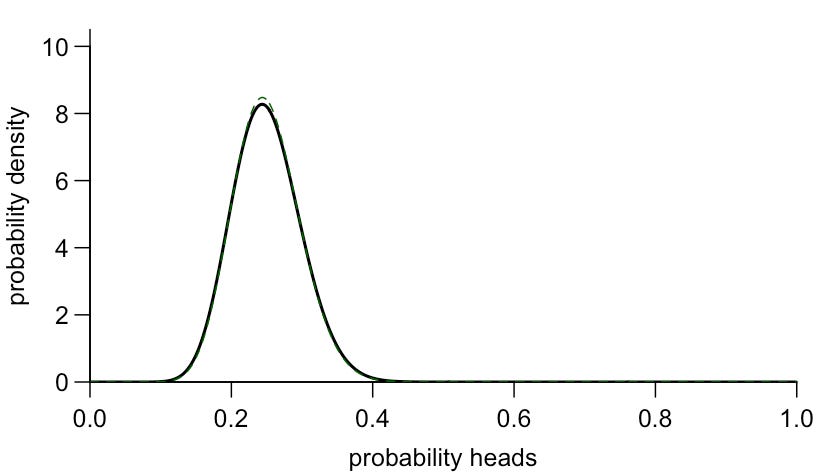
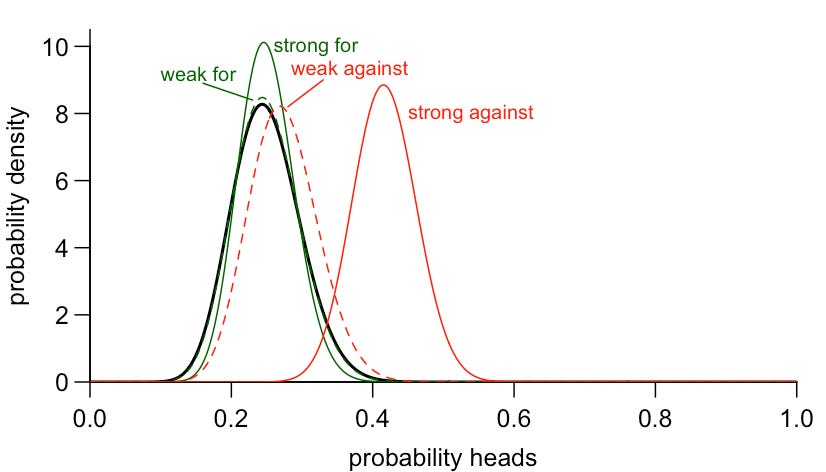
So far we’ve been looking at situations where the evidence runs counter to what we believe. Depending on the strength of that evidence, we either saw a small or quite noticeable shift in posterior belief. Now, suppose that we flipped the coin and it came up tails 3 times out of 4. This is exactly the ratio our prior belief would predict, so it should strengthen our belief. But Bayes’ theorem tells us this should only strengthen it very slightly:

But what if we had observed 30 tails out of 40 flips? This strengthens our belief more, but still not in a way that looks dramatically different to the original prior, or the posterior after seeing some weak evidence:

In other words, the same number of data points (4 or 40 flips) can shift our overall outlook in noticeably different ways depending on whether they run for or against our prior belief:

Beyond coins

Coin flips can be easily measured, but in other areas of life, we won’t necessarily be able to run a simple calculation. Instead, we’ll often encounter arguments, compare them to our prior beliefs, then end up with a certain view afterwards – which may be the same view we had to begin with.

Let’s say you have a strong belief about something. It could be enthusiasm for a particular film, or support for a political party. If you encounter evidence that aligns with your belief, you’ll walk away with a similar view, even if the evidence is weak. But what if someone makes an argument that challenges your belief? If it’s a weak argument, it won’t necessarily alter your opinion, but if it’s a watertight message delivered in a compelling way, it may well shift your attitude.

For example, in 2013, the UK legalised same-sex marriage. A Conservative MP named John Randall voted against the bill, but later said he regretted the decision. If only he’d talked to one of his colleagues beforehand, a man who many might have expected to oppose marriage equality, but actually turned out to support it. ‘He said to me that it was something that wouldn’t affect him at all but would give great happiness to many people,’ Randall said in 2017. ‘That is an argument that I find it difficult to find fault with.’

OK, maybe this post is a bit about politics after all.

Just as the Bayes’ theorem example above suggests, it’s generally easier to see the effect of arguments that we might initially disagree with. I’ve thought about this example quite a lot in recent days and weeks, as people shared content and messages from the presidential candidate they supported. Often there seemed to be a discordance between the strength of the message and the enthusiasm with which it was being shared. (I was also conscious that my own biases and beliefs would in turn be shaping how I thought others might be thinking about these posts.)

This discordance can be a big challenge when it comes to political arguments. Back in 2015, psychologists Matthew Feinberg and Robb Willer ran a study to see whether people could come up with arguments that would persuade those with differing political views. Rather than accounting for the moral position of the person they were trying to persuade, many participants instead created arguments that aligned with their own moral position. Conservatives based their arguments on ideas like loyalty and respect for authority, while liberals appealed to values like equality and social justice.

Although it might be easy to argue from a familiar starting point, it doesn’t seem to be a very effective strategy. The researchers found that persuasion was more likely when participants tailored their arguments to the moral values of the people they disagreed with. This suggests that if you want to persuade a conservative, you’re better off focusing on concepts like patriotism and group loyalty, whereas it’s easier to convince liberals by promoting messages of fairness.

This doesn’t necessarily mean we’ll solve extreme politics just by finding the right moral framing. As I’ve written about previously, we increasingly face the threat of groups who manipulate online interactions to amplify harmful content. We also face the challenge of social media platforms that expose people more to opposing ideologies, but also the most extreme and divisive versions of these ideas, driving deeper polarisation. Meanwhile, attempts to share good science and evidence online struggle against co-ordinated bad faith attacks.

But faced with these challenges, we should also consider our own perceptions of what we’re communicating, and the audiences we are – and aren’t – reaching. Because it may also be the case that, among all these other obstacles, our arguments and messages simply aren’t as effective as we assume they are.

Cover image: Simon via Unsplash