We can't avoid models

Even insights from 'raw data' require assumptions

There’s a simplistic dichotomy that I often see made in science. On one hand, goes the stereotype, we have ‘data-driven’ insights (i.e. pure observations, no models or assumptions involved). And on the other, we have ‘model-driven’ insights (i.e. assumption-laden, theoretical, not data).

But the reality is rarely this simple. For most questions we care about, it is generally impossible to just ‘look at the data’ to get an answer without making some assumptions.

Take the problem of estimating how many people in the population have a particular characteristic (e.g. what proportion are infected with a given virus, or own a given item). Let’s call this proportion P. Unless we can somehow observe everything, everywhere, all at once, we have to make some assumptions if we want to know P.

For example, we might sample 1000 people and see how many have the characteristic. But how do we choose these people? And, how confident can we be that the observed fraction reflects the wider population?

We could try and pick these 1000 people at random. Which leads to the question: how do you pick people randomly? Get a phonebook and ring random phone numbers? Send letters to random addresses? The people who respond won’t necessarily be a random sample of the wider population. And if we assume they are, then we’re implicitly making (strong) assumptions about the sampling process.

Suppose for a moment we did manage to get a near-random selection of 1000 people, and 50 of them (i.e. 5%) have the characteristic of interest. How confident can we be in this estimate? After all, we may have picked more – or less – people from certain demographic groups purely by chance.

Random but unbalanced

The logic behind choosing people at random is that, on average, we’d expect to get an unbiased estimate of the true population mean. But this is on average. Although randomness helps us across many theoretical samples, a single sample won’t necessary reflect the true extent of the characteristic in the wider population.

One option to quantify our uncertainty is to calculate a simple binomial confidence interval. The smaller the sample, the larger the uncertainty will be (see my previous post for some rules of thumb here). But we still have to choose a method to calculate this ‘simple’ interval. If 50 out of 1000 people have a given characteristic, the popular ‘Wilson score’ method gives us a 95% confidence interval of 3.77% to 6.59%, whereas the also popular ‘Clopper–Pearson interval’ gives us 3.73% to 6.54%¹.

The decisions don’t end there. A confidence interval is based on hypothetically picking random samples again and again; if we were to do this, goes the theory, 95% of the measured confidence intervals would contain the true value. But in reality, we only have one sample to work with (i.e. the one we collected). And looking at the sample, we might notice that it is unbalanced in some obvious ways. Perhaps there are too many young people in our sample relative to the overall population, for example. If the characteristic is likely to be more common among young people, this will bias our estimate.

We could address this issue by weighting our sample according to groups that we think are likely to be important in shaping whether someone has a particular characteristic. For example, we might decide to adjust for things like age, ethnic background, education level and geographic location. But if we adjust for these things, we are imposing an implicit model on our estimate. In effect, we are saying that we think these factors are more predictive of having the characteristic than the other factors we aren’t adjusting for.

To illustrate the challenge, imagine we’ve collected a sample that happens to contain more people with long names than the wider population, but correctly represents the age distribution of the population. If age is the dominant driver of whether a person will have the characteristic we’re interested in – and name length is irrelevant – then if we adjust for name length, but not age, it would make our estimate worse (because at the moment it’s balanced according to what matters). In other words, we’ve chosen an inappropriate model that pulls us further away from reality.²

Implausibly noisy

Now suppose we’ve ironed out the problems above, or at least made assumptions that we’re reasonably happy with. Then we decide to run our survey a few times to see how things change over time. In the first large survey, we estimate 50% have the characteristic (after adjusting for factors we thing are important to balance). But the next week, our estimate drops to 30%. And the week after, it jumps back to 55%. Because the surveys are large, the confidence intervals are narrow, so it doesn’t seem to be a purely chance result. Is it really plausible that the percentage of people with the characteristic has jumped up and down so much?

It helps to think about the process that generates what we’re measuring. Suppose once people gain this particular characteristic, they retain it for a few weeks on average. If we’re looking at infections, it might be that people test positive for a while; if we’re looking at perishable products, it might be that people don’t hang on to them for very long. As a result, let’s say that a given person has the following probability of retaining this hypothetical characteristic over time:

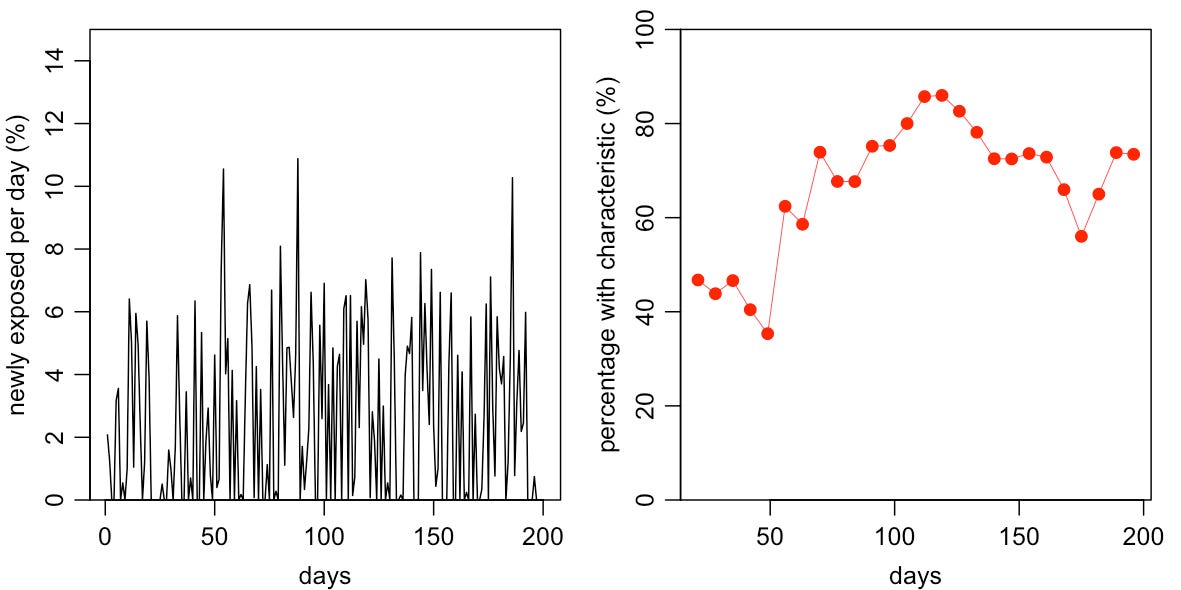
This curve will have the effect of ‘smoothing over’ the number of people with the characteristic at a given point in time. This is because the characteristic we measure in a weekly survey is the accumulation of multiple earlier, noisy events. For example, suppose the percentage of people exposed on a given day is very random (left plot below). The resulting percentage with the characteristic each week will generally be smoother and more predictable (shown in right plot below):

In this scenario, it’s therefore not so plausible that the percentage with the characteristic would jump around dramatically each week, because the process that generates the data generally does not produce a pattern this noisy. So not only it is helpful here to use a model that accounts for the underlying dynamics of the characteristic – we would be making a mistake to not account for these dynamics.

Models are inevitable, so we must embrace them

The above shows that it’s useful to think more deeply about what we’re measuring, and the processes behind these measurements. Even apparently simple estimates require a model with several assumptions. Made hastily (or unknowingly), these modelling assumptions can potentially bias our estimates. On the other hand, if constructed carefully, such models can help reduce the risk of bias and incorrect conclusions.

When faced with difficult decisions, there can be a tendency to prefer inaction over action (i.e. omission bias). But just as doing nothing is making a decision, not making explicit assumptions still means making assumptions.

In reality, there is no distinction between ‘model-based analysis’ and ‘model-free analysis’. There are just models, with varying degrees of complexity and transparency. Which means that, in practice, the main distinction is between people who write down and discusses their modelling assumptions – and those who don’t.

1. If you use the prop.test() function in R, you’re using the Wilson score; if you use binom.test(), you’re using Clopper-Pearson.

2. I edited this example after some useful discussion with Tim Morris (see the comments), as I realised the first version could have been clearer in communicating a hypothetical situation where adjusting for the wrong thing can make our estimate worse. His recent post has more discussion about when adjustment can be helpful rather than harmful.